![\includegraphics[height=10cm]{sombr}](img1.png)
Hubert Selhofer, revised by Marcel Oliver
updated to
current Octave version by Thomas L. Scofield
Date: 2008/08/16
![\includegraphics[height=10cm]{sombr}](img1.png)
Octave is an interactive programming language specifically suited for vectorizable numerical calculations. It provides a high level interface to many standard libraries of numerical mathematics, e.g. LAPACK or BLAS.
The syntax of Octave resembles that of Matlab. An Octave program usually runs unmodified on Matlab. Matlab, being commercial software, has a larger function set, and so the reverse does not always work, especially when the program makes use of specialized add-on toolboxes for Matlab.
octave:1> help eig
| < | smaller | <= | smaller or equal | & | and |
| > | greater | >= | greater or equal | | | or |
| == | equal | ~= |
not equal | ~ |
not |
octave:1> x12 = 1/8, long_name = 'A String' x12 = 0.12500 long_name = A String octave:2> sqrt(-1)-i ans = 0 octave:3> x = sqrt(2); sin(x)/x ans = 0.69846And here is a script doless, saved in a file named doless.m:
one = 1; two = 2; three = one + two;Calling the script:
octave:1> doless octave:2> whos *** local user variables: prot type rows cols name ==== ==== ==== ==== ==== wd real scalar 1 1 three wd real scalar 1 1 one wd real scalar 1 1 two
Matrices and vectors are the most important building blocks for programming in Octave.
v = [ 1 2 3 ]
v = [ 1; 2; 3 ]
Start[:Increment]:End
octave:1> x = 3:6
x =
3 4 5 6
octave:2> y = 0:.15:.7
y =
0.00000 0.15000 0.30000 0.45000 0.60000
octave:3> z = pi:-pi/4:0
z =
3.14159 2.35619 1.57080 0.78540 0.00000
A matrix
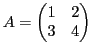 is generated as follows.
is generated as follows.
octave:1> A = [ 1 2; 3 4]
A =
1 2
3 4
Matrices can assembled from submatrices:
octave:2> b = [5; 6];
octave:3> M = [A b]
M =
1 2 5
3 4 6
There are functions to create frequently used
![]() matrices.
If
matrices.
If ![]() , only one argument is necessary.
, only one argument is necessary.
octave:1> A = [1 2; 3 4]; B = 2*ones(2,2);
octave:2> A+B, A-B, A*B
ans =
3 4
5 6
ans =
-1 0
1 2
ans =
6 6
14 14
While * refers to the usual matrix multiplication, .* denotes element-wise multiplication. Similarly, ./ and .^ denote the element-wise division and power operators.
octave:1> A = [1 2; 3 4]; A.^2 % Element-wise power
ans =
1 4
9 16
octave:2> A^2 % Proper matrix power: A^2 = A*A
ans =
7 10
15 22
octave:1> A = [1 2 3; 4 5 6]; v = [7; 8];
octave:2> A(2,3) = v(2)
A =
1 2 3
4 5 8
octave:3> A(:,2) = v
A =
1 7 3
4 8 8
octave:4> A(1,1:2) = v'
A =
7 8 3
4 8 8
A\b solves the equation
Traditionally, functions are also stored in plain text files with suffix .m. In contrast to scripts, functions can be called with arguments, and all variables used within the function are local--they do not influence variables defined previously.
A function f, saved in the file named f.m.
function y = f (x)
y = cos(x/2)+x;
end
In Octave, several functions can be defined in a single script file. Matlab on the other hand, strictly enforces one function per .m file, where the name of the function must match the name of the file. If compatibility with Matlab is important, this restriction should also be applied to programs written in Octave.
A function dolittle, which is saved in the file named dolittle.m.
function [out1,out2] = dolittle (x)
out1 = x^2;
out2 = out1*x;
end
Calling the function:
octave:1> [x1,x2]=dolittle(2) x1 = 4 x2 = 8 octave:2> whos *** currently compiled functions: prot type rows cols name ==== ==== ==== ==== ==== wd user function - - dolittle *** local user variables: prot type rows cols name ==== ==== ==== ==== ==== wd real scalar 1 1 x1 wd real scalar 1 1 x2
Obviously, the variables out1 and out2 were local to dolittle. Previously defined variables out1 or out2 would not have been affected by calling dolittle.
global name declares name as a global variable.
A function foo in the file named foo.m:
global N % makes N a global variable; may be set in main file function out = foo(arg1,arg2) global N % makes local N refer to the global N <Computation> endIf you change N within the function, it changes in the value of N everywhere.
The syntax of for- and while-loops is immediate from the following examples:
for n = 1:10
[x(n),y(n)]=dolittle(n);
end
while t<T
t = t+h;
end
For-loop backward:
for n = 10:-1:1 ...
Conditional branching works as follows.
if x==0
error('x is 0!');
else
y = 1/x;
end
switch pnorm
case 1
sum(abs(v))
case inf
max(abs(v))
otherwise
sqrt(v'*v)
end
Approximate an integral by the midpoint rule:
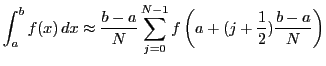
We define two functions, gauss.m and mpr.m, as follows:
function y = gauss(x)
y = exp(-x.^2/2);
end
function S = mpr(fun,a,b,N)
h = (b-a)/N;
S = h*sum(feval(fun,[a+h/2:h:b]));
end
Now the function gauss can be integrated by calling:
octave:1> mpr('gauss',0,5,500)
Loops and function calls, especially through feval, have a very high computational overhead. Therefore, if possible, vectorize all operations.
We are programming the midpoint rule from the previous section
with a for-loop (file name is mpr_long.m):
function S = mpr_long(fun,a,b,N)
h = (b-a)/N; S = 0;
for k = 0:(N-1),
S = S + feval(fun,a+h*(k+1/2));
end
S = h*S;
end
We verify that mpr and mpr_long yield the same answer,
and compare the evaluation times.
octave:1> t = cputime;
> Int1=mpr('gauss',0,5,500); t1=cputime-t;
octave:2> t = cputime;
> Int2=mpr_long('gauss',0,5,500); t2=cputime-t;
octave:3> Int1-Int2, t2/t1
ans = 0
ans = 45.250
octave:1> for k = .1:.2:.5,
> fprintf('1/%g = %10.2e\n',k,1/k); end
1/0.1 = 1.00e+01
1/0.3 = 3.33e+00
1/0.5 = 2.00e+00
Procedure for plotting a function ![]() :
:
x = x_min:step_size:x_max;(See also Section 2.1.)
y = f(x);Important: Since
plot(x,y)
plot(x,y) grid
octave:1> x = -10:.1:10; octave:2> y = sin(x).*exp(-abs(x)); octave:3> plot(x,y) octave:4> grid
![\includegraphics[height=7cm]{2d-plot1}](img35.png)
octave:1> x = -2:0.1:2; octave:2> [xx,yy] = meshgrid(x,x); octave:3> z = sin(xx.^2-yy.^2); octave:4> mesh(x,x,z);
![\includegraphics[height=8cm]{3d-plot1}](img36.png)
Take a matrix ![]() and a vector
and a vector ![]() with
with
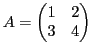 and
and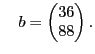
Solve the system of equations
A = reshape(1:4,2,2).'; b = [36; 88]; A\b [L,U,P] = lu(A) [Q,R] = qr(A) [V,D] = eig(A) A2 = A.'*A; R = chol(A2) cond(A)^2 - cond(A2)
Compute the matrix-vector product of a
![]() random matrix
with a random vector in two different ways. First, use the built-in
matrix multiplication *. Next, use for-loops.
Compare the results and computing times.
random matrix
with a random vector in two different ways. First, use the built-in
matrix multiplication *. Next, use for-loops.
Compare the results and computing times.
A = rand(100); b = rand(100,1);
t = cputime;
v = A*b; t1 = cputime-t;
w = zeros(100,1);
t = cputime;
for n = 1:100,
for m = 1:100
w(n) = w(n)+A(n,m)*b(m);
end
end
t2 = cputime-t;
norm(v-w), t2/t1
Running this script yields the following output.
ans = 0 ans = 577.00
Calculate all the roots of the polynomial
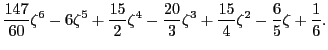
Hint: Use the command compan.
Plot these roots as points in the complex plane and draw a unit circle for comparison. (Hint: hold, real, imag).
bdf6 = [147/60 -6 15/2 -20/3 15/4 -6/5 1/6];
R = eig(compan(bdf6));
plot(R,'+'); hold on
plot(exp(pi*i*[0:.01:2]));
if any(find(abs(R)>1))
fprintf('BDF6 is unstable\n');
else
fprintf('BDF6 is stable\n');
end
![\includegraphics[height=8cm]{bdf6}](img44.png)
Plot the graph of the function
x = -3:0.1:3;
[xx,yy] = meshgrid(x,x);
z = exp(-xx.^2-yy.^2);
figure, mesh(x,x,z);
title('exp(-x^2-y^2)');
For each
![]() Hilbert matrix
Hilbert matrix ![]() where
where
![]() compute
the solution to the linear system
compute
the solution to the linear system ![]() ,
, ![]() ones(n,1). Calculate the error and the condition number of
the matrix and plot both in semi-logarithmic coordinates. (Hint:
hilb, invhilb.)
ones(n,1). Calculate the error and the condition number of
the matrix and plot both in semi-logarithmic coordinates. (Hint:
hilb, invhilb.)
err = zeros(15,1); co = zeros(15,1);
for k = 1:15
H = hilb(k);
b = ones(k,1);
err(k) = norm(H\b-invhilb(k)*b);
co(k) = cond(H);
end
semilogy(1:15,err,'r',1:15,co,'x');
Calculate the least square fit of a straight line to the points
![]() , given as two vectors
, given as two vectors ![]() and
and ![]() . Plot the points and
the line.
. Plot the points and
the line.
function coeff = least_square (x,y)
n = length(x);
A = [x ones(n,1)];
coeff = A\y;
plot(x,y,'x');
hold on
interv = [min(x) max(x)];
plot(interv,coeff(1)*interv+coeff(2));
end
Write a program to integrate an arbitrary function ![]() in one variable
on an interval
in one variable
on an interval ![]() numerically using the trapezoidal rule with
numerically using the trapezoidal rule with
![]() :
:
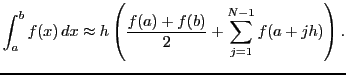
For a function
function S = trapez(fun,a,b,N)
h = (b-a)/N;
% fy = feval(fun,[a:h:b]); better:
fy = feval(fun,linspace(a,b,N+1));
fy(1) = fy(1)/2;
fy(N+1) = fy(N+1)/2;
S = h*sum(fy);
end
function y = f(x)
y = exp(x);
end
for k=1:15;
err(k) = abs(exp(1)-1-trapez('f',0,1,2^k));
end
loglog(1./2.^[1:15],err);
hold on;
title('Trapezoidal rule, f(x) = exp(x)');
xlabel('Increment');
ylabel('Error');
loglog(1./2.^[1:15],err,'x');